基礎理論
集合
集合とは、ある明確な条件のもとにグループ化されたデータの集まりのことです。
ベン図を利用して視覚的に表現できます。また集合の演算には論理演算を適用できます。
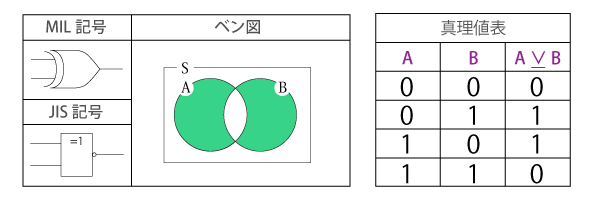
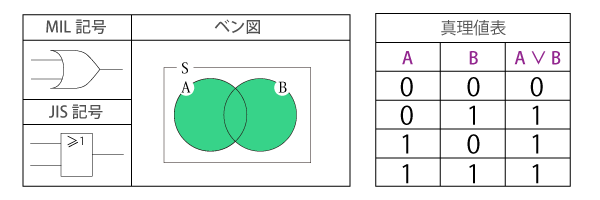
論理和(OR)
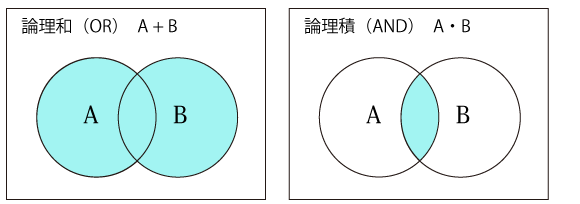
AとBの少なくともいずれかを含む部分で、「AまたはB」の関係を表します。
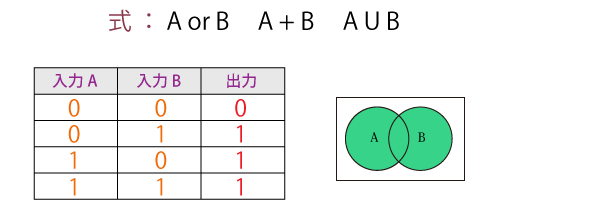
二項演算であり、入力された論理のどちらか一方でも真値(true)なら真値が出力され、そうでなければ偽(false)が出力されます。
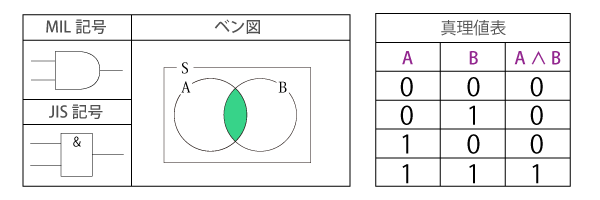
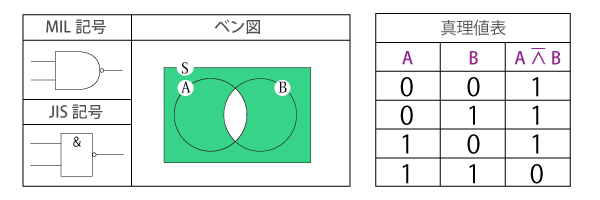
論理積(AND)
AとBの両方を含む部分で、「AかつB」の関係を表します。
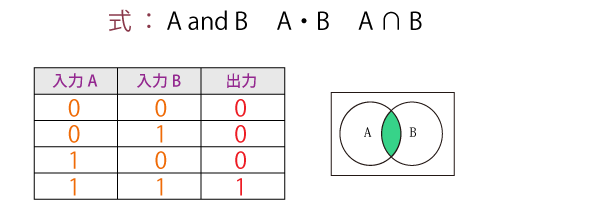
二項演算であり、入力された論理の両方が真(true)の場合のみ真値が出力され、さもなくば偽(false)が出力されます。
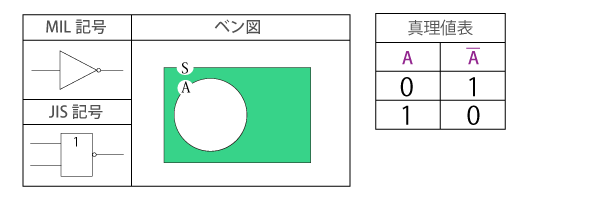
否定(NOT)
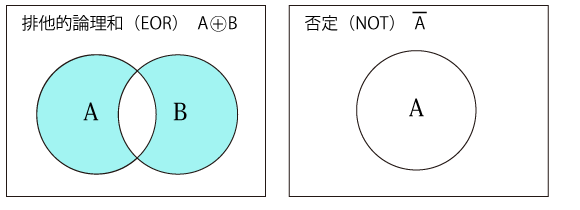
Aを含まない部分で、「Aではない」関係を表します。
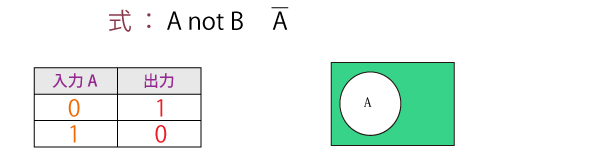
単項演算であり、入力された論理が無条件に反転して出力されます。
否定論理積(NAND)
論理積(AND)の出力を否定(NOT)したもので、「(AかつB)ではない」の関係を表します。
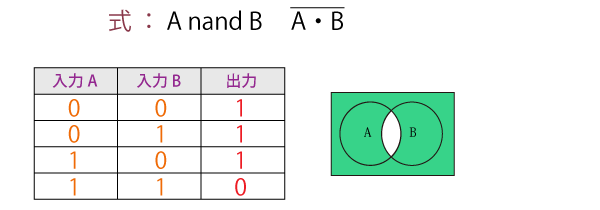
二項演算であり、入力された論理の双方が真(true)なら偽(false)が出力され、さもなくば真(true)が出力されます。
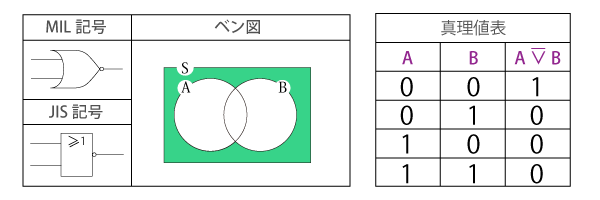
否定論理和(NOR)
論理和(OR)の出力を否定(NOT)したもので、「(AまたはB)ではない」の関係を表します。
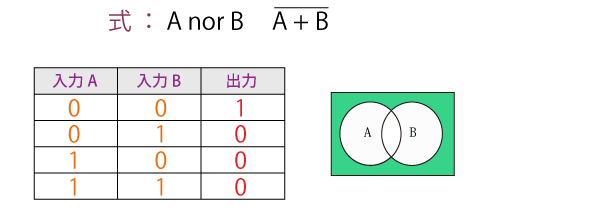
二項演算であり、入力された論理のどちらか一方でも真(true)なら偽(false)が出力され、さもなくば真が出力されます。
排他的論理和(XOR、EOR)
入力値が異なる場合に1を出力し、それ以外の場合(入力値が同じとき)には0を出力します。
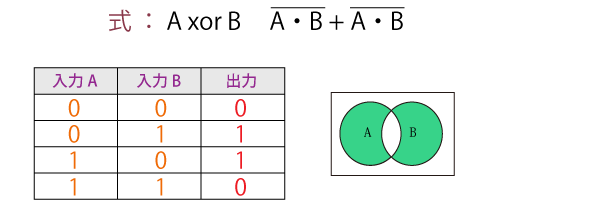
一般には二項演算ですが、二つ以上であれば、その数は問いません。
二つ以上の入力のうち、真(true)が奇数個なら真(true)、偶数個なら偽(false)を返します。