応用数学
符号理論、A/D変換、量子化誤差
符号理論
情報を符号化して通信を行う際の効率と信頼性についての理論です。
符号は以下の2種類に分けられます。
① 情報源符号(データ圧縮: コンパクト符号など)
② 伝送路符号(誤り検出訂正: ブロック符号、畳み込み符号、前方誤り訂正(FEC)など)
情報源符号化は、情報源で転送前のデータをより効率的に圧縮することを目指し、この成果はインターネット上でのデータ圧縮形式としてよく見かけます。
伝送路符号化は、余分なデータビット(冗長ビット)を付与することで、通信路上に存在する雑音などの障害への耐性を強化します。この技術はあまり目立ちませんが、例えば音楽CDではリード・ソロモン符号を使って傷や埃による誤りを訂正しています。
A/D変換
A/D変換とは、アナログの信号をデジタルの信号に置き換える操作のことです。

- » 標本化→アナログ信号を一定間隔で切り取る
- » 量子化→切り取った信号の大きさを有限精度の数字とする
- » 符号化→読み取った数値を符号化する
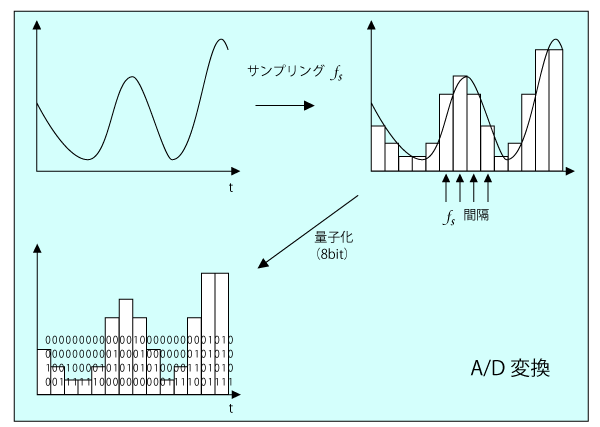
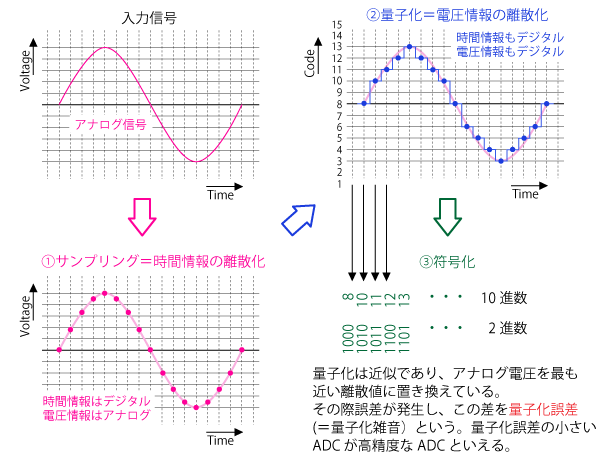
AD変換とは、① サンプリング→ ② 量子化→ ③ 符号化のことを言います。
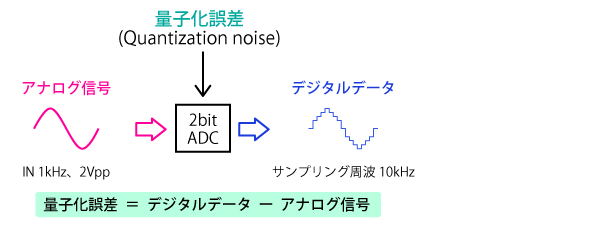
量子化誤差
AD変換を行うと必ず発生する、アナログ信号とデジタルデータのズレが量子化誤差です。
ADCの電圧分解能を上げることで、量子化誤差を小さくすることができます。