基礎理論
ド・モルガンの法則
「ド・モルガンの法則」とは、AND演算とOR演算を相互に変換するものです。
左辺のAND演算を右辺のOR演算に変換したり、左辺のOR演算を右辺のAND演算に変換します。
ド・モルガンの法則に相当するものは、四則演算にはありません。論理演算ならではの法則です。
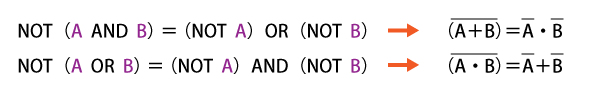
AND演算も見方によってはOR演算に見え、OR演算も見方によってはAND演算に見える」ということです。
この見方とは、これまで真理値表の1を真、0を偽と見てきましたが(これを「正論理」と呼びます)、逆転の発想で0を真、1を偽と見る(これを「負論理」と呼びます)ことです。
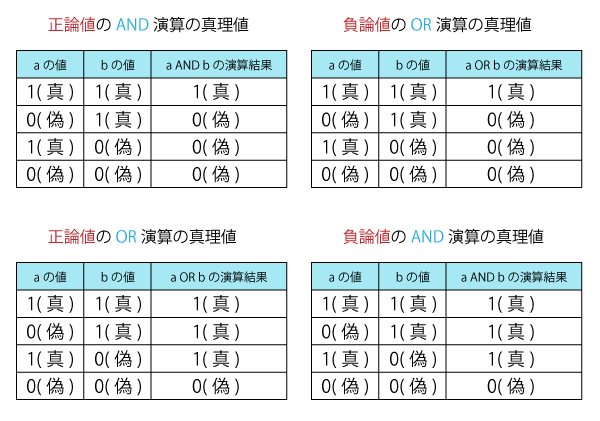
NOT演算は、1と0を反転させるものです。
NOT(a AND b)=(NOT a)OR(NOT b)は、aとbを反転させると、AND演算の演算結果の反転が、OR演算の演算結果になることを意味しています。
NOT(a OR b)=(NOT a)AND(NOT b)は、aとbを反転させると、OR演算の演算結果の反転が、AND演算の演算結果になることを表しています。
