基礎理論
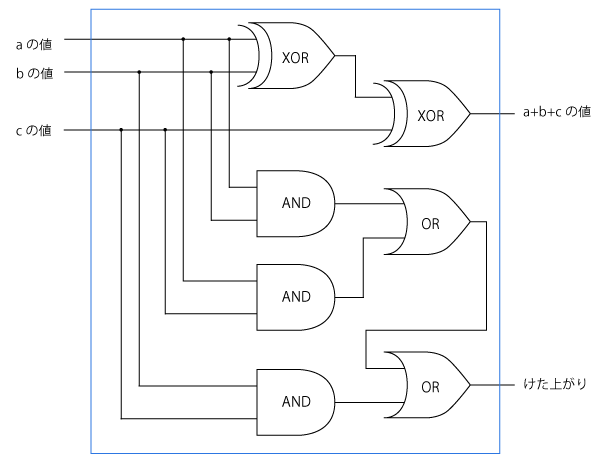
全加算回路
下位からの桁上がり、上位への桁上げをともに考慮した加算回路のことをいいます。
2つの入力と下位からの桁上がりに対して演算を行い、その桁の和と桁上げを出力します。
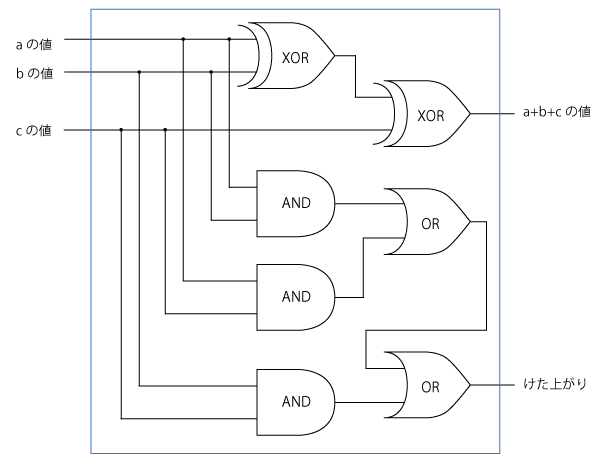
下位けたからのけた上がりを含めて、加算が行える回路を「全加算回路(full adder)」と呼びます。
全加算回路は、入力が3つあり、該当するけたの2つの値と、下位けたからけた上がりした値で3つです。
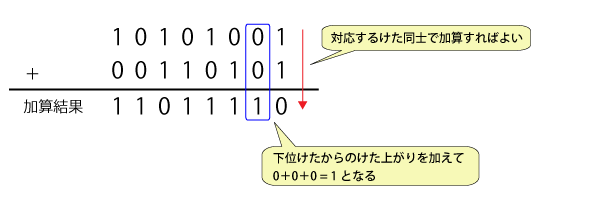
全加算回路の3つの入力と演算結果を表3に示します。
cは下位けたからのけた上がりです。
表をよく見て、a+b+cとそのけた上がりがどのような論理演算の組み合せで表せるか考えてみましょう。
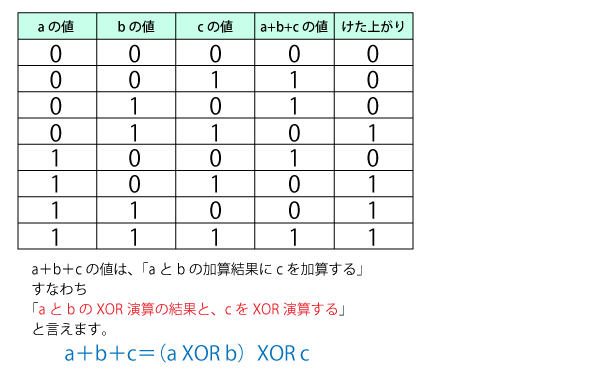
けた上がりは、「a、b、cの中で1であるものが少なくとも2つある」すなわち「aとbが1、またはaとcが1、またはbとcが1」となります。
けた上がり=(a AND b)OR(a AND c)OR(b AND c)