応用数学
待ち行列理論(M/M/1)
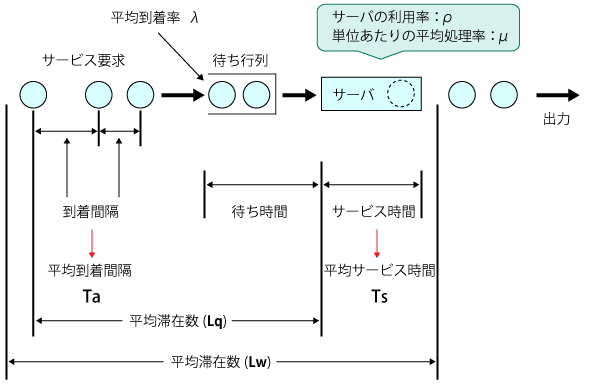
例えば、1台のネットワーク・プリンタに複数の要求が並んで順番を待っています。
このとき、要求を送信してから印刷が完了するまでの時間は「(プリンタが使用可能になるのを)待っている時間」、「プリンタを使用している時間」、「その他の時間(通信時間など)」の合計になります。
ここで待っている時間と、使用している時間、および要求が到着する間隔に着目して、これらの関係を理論式で推測していくのが待ち行列理論です。
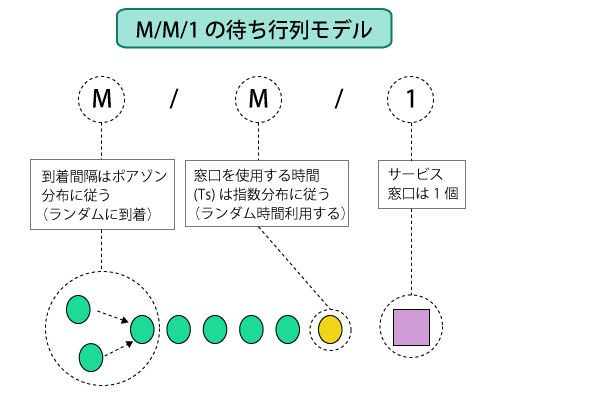
M/M/1というのはケンドールの記法で待ち行列のモデルで、以下の三つの条件が成り立っている状態を指します。
① サービス要求の到着間隔がランダム(ポアゾン分布)
② 窓口を使用する時間は要求ごとにランダム(指数分布)
③ 待ち行列のサービス窓口は1個
※ 約束事: 行列へ割り込んだり、列の途中で抜け出すことは考えない。
サービス要求は到着順に受け付ける。
利用率と到着率とサービス率
利用率をρ(ロー)、到着率をλ(ラムダ)、サービス率をμ(ミュー)とした場合、次の式が成り立ちます。
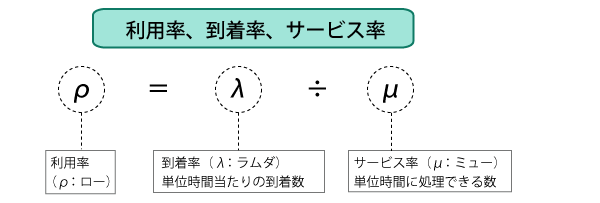
例えば、Webサーバへのアクセスの単位時間を1時間にした場合、到着するサービス要求が12件、サーバーが処理できる要求数が20件だった場合の利用率は、12÷20=0.6ということになります。
M/M/1の公式
M/M/1の待ち行列において、待ち時間をTw、平均サービス時間をTsとしたとき、次の式が成り立ちます。

例えば、利用率が0.6で平均サービス時間が3分の場合、上記の式に当てはめると、
0.6÷(1-0.6)×3(分)= 4.5(分)となります。
- トランザクション数又は平均到着率 λ =単位時間に到着する客数の平均値
- 平均サービス率 μ =単位時間にサービスを受ける客数の平均値
- 平均サービス時間 Ts =1/ μ
- 平均到着間隔 Ta =1/ λ
- 窓口利用率 ρ = λ/ μ
- 平均待ち行列時間 Tw = ρ× Ts/(1- ρ)
- 待ち行列の平均長さ Lw = ρ2/(1- ρ)= λ× Tw
- 平均待ち(応答)時間 Tq = Ts /(1- ρ)= Tw+ Ts
- 待ち系の平均長さ Lq = ρ/(1- ρ)= Lw+ λ/ μ