グラフ理論とは現実世界の様々な要素を「点」に置き換え、その関係性を「辺」で結び特徴を分析する手法です。

グラフ理論で言う「グラフ」とは、「点」と点同士を結ぶ「辺」から構成されるものを意味します。

グラフは点と点の"つながり方"を表すものであり、個々の点をデータと考えれば、グラフはデータとデータの関係性を表していると言えます。

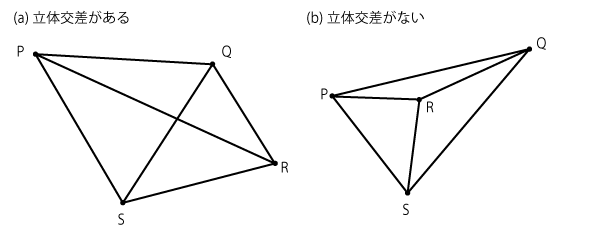
下図の（a）と（b）のグラフは形こそ違うものの、グラフが示す意味は同じです。なぜなら、（a）の点Rをつまんで上に持ち上げた状態が（b）のグラフとなるからです。

1つの点に付いている辺の数を、「次数（じすう）」と呼びますが、例えば、下図の（a）と（b）における点Pの次数はどちらも3ということになります。

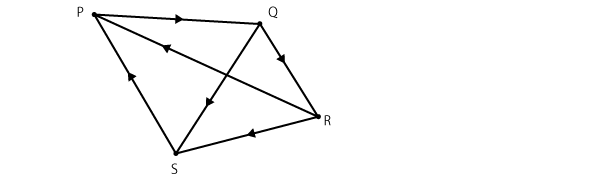
辺の向きを考えたグラフは「有向グラフ」（下図）と呼ぶのに対し、辺の向きを考慮していないグラフを「無向グラフ」と呼びます。

有向グラフは一方通行の道路のようなもので、辺に矢印を付けることで示され、点に入ってくる辺の数「入次数（いりじすう）」と、点から出ていく辺の数「出次数（でじすう）」を区別しています。

下図の例で言えば、点Pの入次数は 2 で、出次数は 1 となります。

グラフの性質

1つ目の性質は、「あらゆるグラフは、次数の合計が偶数になる」というものです。
なぜなら、1つの辺には2つの点（始点と終点）があるため、次数の合計は必ず「辺の数×2」となるといえます。

もう1つの性質は、「あらゆるグラフは、奇数の次数を持つ点が偶数個ある」というものです。
これは1つ目の性質とも関連しますが、奇数の次数を持つ点が奇数個あるとしたら、次数の合計は奇数になってしまいます。よって、奇数の次数を持つ点は必ず偶数個になるのです。